Zadanie nr 3307570
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 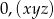 . Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka  jest więc równy
jest więc równy
A) 79 B) 273 C) 237 D) 244
Rozwiązanie
Wyznaczamy cyfry 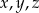 . Ponieważ cyfry okresu powtarzają się co 3, na miejscu 16 po przecinku stoi ta sama cyfra co na miejscu
. Ponieważ cyfry okresu powtarzają się co 3, na miejscu 16 po przecinku stoi ta sama cyfra co na miejscu 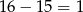 , czyli
, czyli  . Zatem
. Zatem 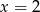 . Podobnie, na miejscach 23 i 18 stoją te same cyfry, co odpowiednio na miejscach 2 i 3. Zatem
. Podobnie, na miejscach 23 i 18 stoją te same cyfry, co odpowiednio na miejscach 2 i 3. Zatem 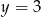 i
i 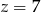 , czyli
, czyli
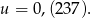
Zamieńmy tę liczbę na ułamek zwykły.
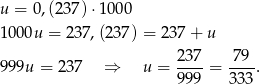
Ponieważ 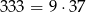 otrzymany ułamek jest nieskracalny, czyli szukany licznik to 79.
otrzymany ułamek jest nieskracalny, czyli szukany licznik to 79.
Odpowiedź: A

