Zadanie nr 1986821
Wskaż rysunek, który może przedstawiać zbiór rozwiązań nierówności 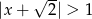 .
.
Rozwiązanie
Sposób I
Liczba 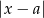 jest równa odległości liczb
jest równa odległości liczb  i
i  na osi liczbowej. Zatem nierówność
na osi liczbowej. Zatem nierówność
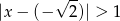
jest spełniona przez liczby  , których odległość od
, których odległość od 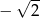 jest większa od 1. Jest to więc zbiór
jest większa od 1. Jest to więc zbiór
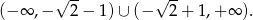
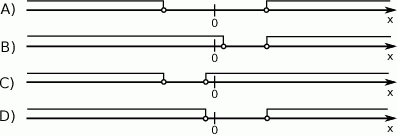
Ponieważ 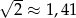 , tylko rysunek C może przedstawiać zbiór rozwiązań.
, tylko rysunek C może przedstawiać zbiór rozwiązań.
Sposób II
Rozwiązujemy nierówność
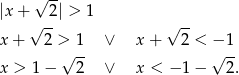
Jak poprzednio zauważamy, że musi to być obrazek C.
Odpowiedź: C

