Zadanie nr 4152037
Zbiór 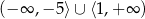 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 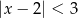 B)
B) 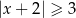 C)
C) 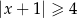 D)
D) 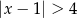
Rozwiązanie
Sposób I
Jeżeli zaznaczymy na osi podany zbiór,
to widać, że jest to zbiór liczb, które są odległe od 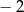 o nie mniej niż 3. Jest to więc zbiór rozwiązań nierówności
o nie mniej niż 3. Jest to więc zbiór rozwiązań nierówności
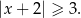
Sposób II
Przypomnijmy, że nierówność 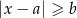 jest równoważna dwóm nierównościom
jest równoważna dwóm nierównościom
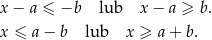
W naszej sytuacji mamy
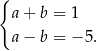
Mamy stąd (np. dodając równania stronami) 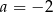 ,
, 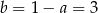 . Podany zbiór jest więc zbiorem rozwiązań nierówności
. Podany zbiór jest więc zbiorem rozwiązań nierówności
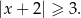
Odpowiedź: B

