Zadanie nr 4166040
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 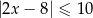 .
.
![]()
Stąd wynika, że
A) 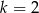 B)
B) 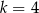 C)
C) 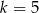 D)
D) 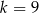
Rozwiązanie
Przekształćmy odrobinę daną nierówność
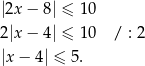
Sposób I
Skorzystamy z interpretacji geometrycznej zbioru rozwiązań nierówności:
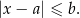
Zbiór ten składa się z liczb, które są odległe (na osi liczbowej) od liczby  o nie więcej niż
o nie więcej niż 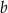 . W naszej sytuacji nierówność opisuje zbiór liczb, które są odległe od 4 o nie więcej niż 5, czyli przedział
. W naszej sytuacji nierówność opisuje zbiór liczb, które są odległe od 4 o nie więcej niż 5, czyli przedział
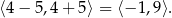
Zatem 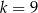 .
.
Sposób II
Rozwiązujemy daną nierówność
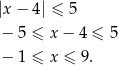
Zatem 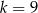 .
.
Odpowiedź: D

