Zadanie nr 4381508

Ile jest liczb całkowitych wśród rozwiązań nierówności 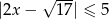√ --- |2x − 17| ≤ 5 ?
A) 5 B) 4 C) 6 D) 7

Rozwiązanie

Sposób I

Przekształćmy daną nierówność

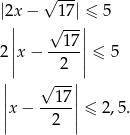
√ --- |2x| − 17||≤ 5 | √ 17| 2 ||x − ----|| ≤ 5 | 2 | || √ --|| ||x − --17|| ≤ 2,5. | 2 |

Rozwiązaniem nierówności są więc liczby, które są odległe od 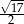√ -- --17- 2 o nie więcej niż 2,5. Jest to więc przedział

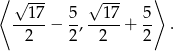
⟨ √ --- √ --- ⟩ --17-− 5,--17-+ 5- . 2 2 2 2

Ponieważ

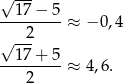
√ --- 17− 5 ---------≈ − 0,4 √ -2- --17+--5- 2 ≈ 4,6 .

nierówność spełnia 5 liczb całkowitych: 0,1,2,3,4.

Sposób II

Liczymy

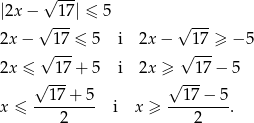
√ --- |2x − 17| ≤ 5 √ --- √ --- 2x− 17 ≤ 5 i 2x− 17 ≥ − 5 2x ≤ √ 17-+ 5 i 2x ≥ √ 17-− 5 √ --- √ --- 17 + 5 17− 5 x ≤ ----2---- i x ≥ ---2----.

Zatem zbiorem rozwiązań nierówności jest przedział

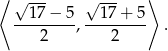
⟨ √ --- √ --- ⟩ 17− 5 17 + 5 --------,--------- . 2 2

Jak w I sposobie stwierdzamy, że w przedziale tym jest 5 liczb całkowitych.
Odpowiedź: A