Zadanie nr 5019731
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 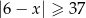 B)
B) 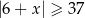 C)
C) 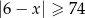 D)
D) 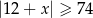
Rozwiązanie
Skorzystamy z interpretacji geometrycznej zbioru rozwiązań nierówności:
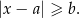
Zbiór ten składa się z liczb, które są odległe (na osi liczbowej) od liczby  o nie mniej niż
o nie mniej niż 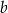 .
.
Środkiem przedziału o końcach -43 i 31 jest 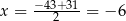 i punkt ten jest odległy od -43 (oraz od 31) o 37. Zatem zaznaczony zbiór to zbiór liczb, które są odległe od -6 o co najmniej 37.
i punkt ten jest odległy od -43 (oraz od 31) o 37. Zatem zaznaczony zbiór to zbiór liczb, które są odległe od -6 o co najmniej 37.
![]()
Zbiór ten jest więc rozwiązaniem nierówności
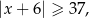
która jest równoważna nierówności 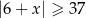 .
.
Odpowiedź: B

