/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Punkty na wykresie

Zadanie nr 2716672

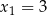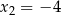Funkcja kwadratowa o miejscach zerowych x1 = 3 i x2 = − 4 , której wykres przechodzi przez punkt 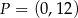P = (0,12) ma wzór:
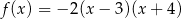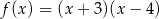
A) f (x) = − 2(x − 3)(x + 4) B) f (x) = (x + 3)(x − 4)
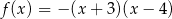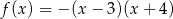
C) f(x ) = − (x+ 3)(x − 4) D) f (x) = − (x − 3)(x + 4)

Wersja PDF

Rozwiązanie

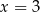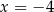Funkcja kwadratowa, która zeruje się dla x = 3 i x = − 4 ma postać

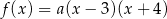
f (x) = a(x − 3)(x + 4 )

(postać iloczynowa). Współczynnik a wyliczamy wstawiając do tego wzoru współrzędne punktu P .

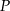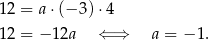
1 2 = a ⋅(− 3)⋅4 1 2 = − 12a ⇐ ⇒ a = − 1.

 
Odpowiedź: D

Wersja PDF