Zadanie nr 1853806
Współrzędne wierzchołka paraboli będącej wykresem funkcji 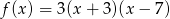 są równe
są równe
A) 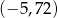 B)
B) 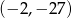 C)
C) 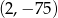 D)
D) 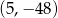
Rozwiązanie
Z podanego wzoru widać, że pierwiastkami trójmianu są liczby 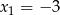 i
i 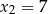 . Wierzchołek paraboli będącej wykresem tej funkcji znajduje się dokładnie w środku między pierwiastkami, czyli
. Wierzchołek paraboli będącej wykresem tej funkcji znajduje się dokładnie w środku między pierwiastkami, czyli
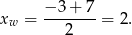
Druga współrzędna jest równa
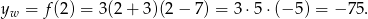
Wierzchołek ma więc współrzędne 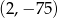 .
.
Sposób II
Przekształcamy podany wzór funkcji.
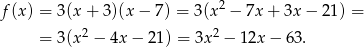
Korzystamy ze wzoru na współrzędne wierzchołka
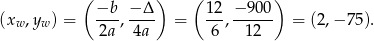
Odpowiedź: C

