Zadanie nr 3364721
Wykresem funkcji kwadratowej 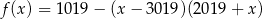 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 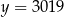 B)
B) 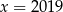 C)
C) 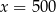 D)
D) 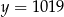
Rozwiązanie
Wierzchołek paraboli 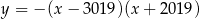 leży na jej osi symetrii, czyli na prostej
leży na jej osi symetrii, czyli na prostej
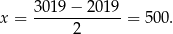
Dana parabola 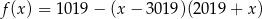 powstaje z powyższej paraboli przez przesunięcie o 1019 jednostek do góry. Pierwsza współrzędna wierzchołka przy tej operacji nie ulegnie zmianie.
powstaje z powyższej paraboli przez przesunięcie o 1019 jednostek do góry. Pierwsza współrzędna wierzchołka przy tej operacji nie ulegnie zmianie.
Odpowiedź: C

