Zadanie nr 7484911
Wskaż wartość parametru 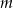 , dla którego prosta
, dla którego prosta 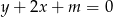 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 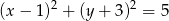
A) 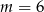 B)
B) 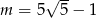 C)
C) 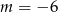 D)
D) 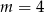
Rozwiązanie
Dane równanie opisuje okrąg o środku 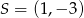 i promieniu
i promieniu 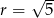 . Szkicujemy tę sytuację
. Szkicujemy tę sytuację
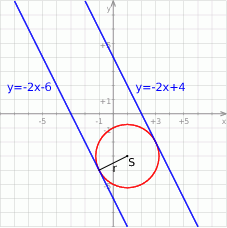
Dana prosta jest styczna do tego okręgu, gdy środek okręgu 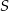 jest od niej odległy o
jest od niej odległy o 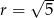 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 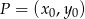 od prostej
od prostej 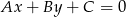 :
:
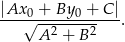
W naszej sytuacji mamy
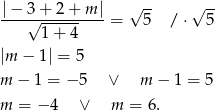
Odpowiedź: A

