/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg/Punkty wspólne z prostymi

Zadanie nr 8018190

Dany jest okrąg 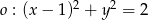2 2 o : (x− 1) + y = 2 i prosta 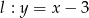l : y = x − 3 . Wskaż zdanie prawdziwe.
A) Prosta 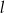l przechodzi przez środek okręgu.
B) Prosta 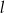l jest rozłączna z okręgiem.
C) Prosta 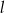l jest styczna do okręgu.
D) Prosta 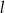l ma z okręgiem dwa punkty wspólne.

Wersja PDF

Rozwiązanie

Środek danego okręgu ma współrzędne 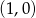(1,0) , więc widać, że nie leży on na podanej prostej. Aby sprawdzić ile punktów wspólnych mają prosta i okrąg podstawiamy 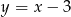y = x − 3 do równania okręgu

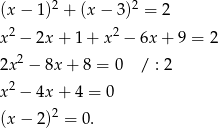
(x − 1)2 + (x − 3)2 = 2 2 2 x − 2x + 1 + x − 6x + 9 = 2 2x2 − 8x + 8 = 0 / : 2 2 x − 4x + 4 = 0 (x − 2)2 = 0.

Widać teraz, że okrąg i prosta mają tylko jeden punkt wspólny, więc są styczne.  
Odpowiedź: C

Wersja PDF