Zadanie nr 4811132
Do okręgu należą punkty 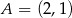 ,
, 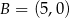 ,
, 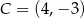 . Jest to okrąg o środku
. Jest to okrąg o środku 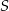 i promieniu
i promieniu  :
:
A) 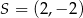 ,
, 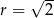 B)
B) 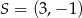 ,
, 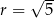
C) 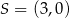 ,
, 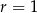 D)
D) 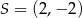 ,
, 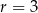
Rozwiązanie
Szkicujemy okrąg, o którym mowa w treści zadania.
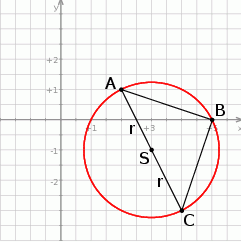
Nawet ze schematycznego rysunku powinno rzucać się w oczy, że trójkąt 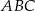 jest prostokątny. Sprawdźmy, że faktycznie tak jest.
jest prostokątny. Sprawdźmy, że faktycznie tak jest.
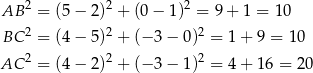
Zatem rzeczywiście 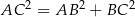 , więc trójkąt
, więc trójkąt 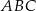 jest prostokątny. Średnicą okręgu opisanego na trójkącie prostokątnym jest przeciwprostokątna, więc
jest prostokątny. Średnicą okręgu opisanego na trójkącie prostokątnym jest przeciwprostokątna, więc
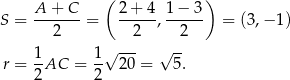
Odpowiedź: B

