/Studia/Analiza/Całki oznaczone/Niewłaściwe/Różne

Zadanie nr 6539876

Oblicz całkę niewłaściwą 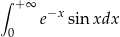∫ +∞ e−x sin xdx 0 .

Wersja PDF

Rozwiązanie

Wyznaczymy funkcję pierwotną całkując dwukrotnie przez części.

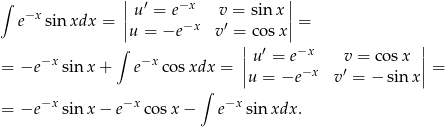
∫ ||u′ = e−x v = sinx || e−x sinxdx = || −x ′ || = u = −e v =|cos x | −x ∫ −x |u ′ = e−x v = cos x | = −e sin x+ e cos xdx = ||u = −e −x v ′ = − sin x|| = ∫ = −e −x sin x− e−xco sx − e−xsin xdx.

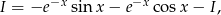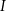Zauważmy, że otrzymaliśmy równanie I = −e −x sinx − e−x cos x− I, gdzie I jest szukaną całką. Stąd 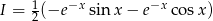1 −x −x I = 2(−e sin x− e cosx ) . Mamy więc funkcję pierwotną

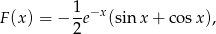
1 F (x) = − --e−x (sinx + co sx), 2

skąd

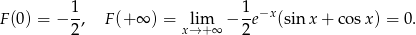
1 1 F (0) = − --, F(+ ∞ ) = lim − -e−x(sin x+ cosx ) = 0. 2 x→ + ∞ 2

Ostatnia granica jest równa 0, bo 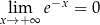−x xli→m+ ∞ e = 0 , a funkcja 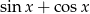sin x + cos x jest ograniczona (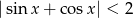|sinx + cosx| < 2 ). Tak więc

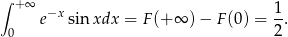
∫ + ∞ 1 e−x sin xdx = F(+ ∞ ) − F(0) = -. 0 2

 
Odpowiedź: 1 2

Wersja PDF