Zadanie nr 1457187
Dane są dwie proste równoległe 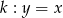 oraz
oraz 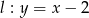 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 1,5 C) 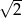 D) 1
D) 1
Rozwiązanie
Rozpoczynamy od szkicowego rysunku
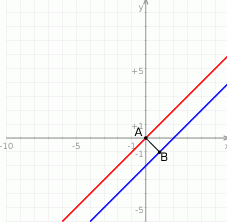
Sposób I
Z obrazka widać, że szukana odległość to np. odległość między punktami 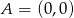 i
i 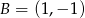 . Jest więc równa
. Jest więc równa
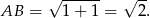
Sposób II
Aby obliczyć odległość między dwoma równoległymi prostymi wystarczy obliczyć odległość dowolnego punktu prostej 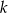 , np.
, np. 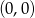 od prostej
od prostej 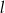 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 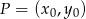 od prostej
od prostej 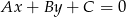 :
:
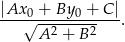
Mamy więc
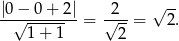
Odpowiedź: C

