/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Proste równoległe

Zadanie nr 1785608

Dodaj do ulubionych
Dodaj do rozwiązanych

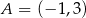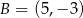Odcinek o końcach A = (− 1,3) i B = (5,− 3) jest równoległy do prostej o równaniu
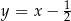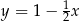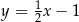A) y = x− 12 B) y = 1 − 12x C) y = 1x− 1 2 D) y = 1 − x 2

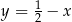
Rozwiązanie

Naszkicujmy odcinek 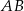AB .

PIC

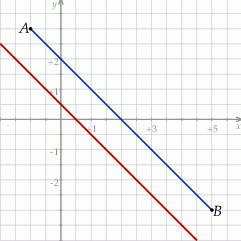
Sposób I

Współczynnik kierunkowy prostej 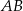AB jest równy

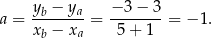
yb −-ya- −-3−-3- a = xb − xa = 5+ 1 = − 1.

Prosta równoległa do prostej 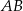AB musi mieć taki sam współczynnik kierunkowy, więc jest to prosta

1- y = 2 − x .

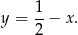
Sposób II

Napiszmy równanie prostej 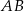AB . Szukamy prostej w postaci 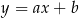y = ax + b i podstawiamy współrzędne punktów 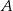A i B .

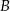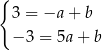
{ 3 = −a + b − 3 = 5a+ b

Odejmujemy od drugiego równania pierwsze i mamy

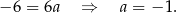
− 6 = 6a ⇒ a = − 1.

Współczynnika 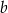b możemy nie obliczać, bo nie jest nam potrzebny. Prosta równoległa do prostej 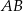AB musi mieć taki sam współczynnik kierunkowy, więc jest to prosta

1 y = --− x . 2

 
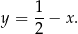
Odpowiedź: D

Wersja PDF