Zadanie nr 2787842
Prosta 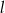 ma równanie
ma równanie 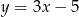 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 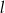 i przechodzącej przez punkt
i przechodzącej przez punkt 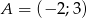 ma postać:
ma postać:
A) 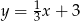 B)
B) 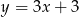 C)
C) 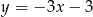 D)
D) 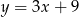
Rozwiązanie
Proste 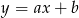 i
i 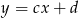 są równoległe wtedy i tylko wtedy, gdy mają równe współczynniki kierunkowe, czyli gdy
są równoległe wtedy i tylko wtedy, gdy mają równe współczynniki kierunkowe, czyli gdy  . W takim razie proste równoległe do danej prostej to proste
. W takim razie proste równoległe do danej prostej to proste 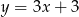 i
i 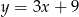 . Pozostało sprawdzić, która z tych prostych przechodzi przez punkt
. Pozostało sprawdzić, która z tych prostych przechodzi przez punkt 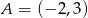 .
.
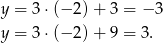
Zatem współrzędne punktu 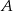 spełniają drugie równanie.
spełniają drugie równanie.
Odpowiedź: D

