Zadanie nr 2938427
Równanie prostej przechodzącej przez punkt 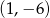 i równoległej do prostej
i równoległej do prostej 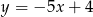 jest dane wzorem
jest dane wzorem
A) 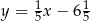 B)
B) 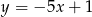 C)
C) 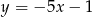 D)
D) 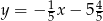
Rozwiązanie
Sposób I
Ponieważ szukana prosta jest równoległa do prostej danej wzorem 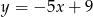 , więc jest dana wzorem
, więc jest dana wzorem 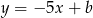 . Liczymy współczynnik
. Liczymy współczynnik 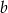
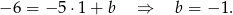
Zatem szukana prosta jest dana wzorem 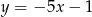 .
.
Sposób II
Jak poprzednio zauważamy, że szukana prosta musi mieć postać 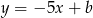 . To eliminuje dwie odpowiedzi. Która z dwóch pozostałych jest poprawna? – sprawdzamy podstawiając współrzędne podanego punktu.
. To eliminuje dwie odpowiedzi. Która z dwóch pozostałych jest poprawna? – sprawdzamy podstawiając współrzędne podanego punktu.
Odpowiedź: C

