Zadanie nr 8366670
Proste o równaniach 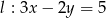 i
i 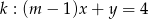 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 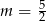 B)
B) 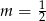 C)
C) 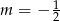 D)
D) 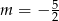
Rozwiązanie
Przypomnijmy, że dwie proste 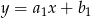 i
i 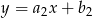 są równoległe jeżeli mają równe współczynniki kierunkowe
są równoległe jeżeli mają równe współczynniki kierunkowe 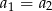 .
.
Przekształćmy podane równania prostych tak, aby było widać jakie są ich współczynniki kierunkowe.
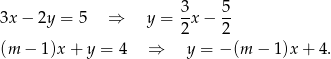
Zatem musi być spełniony warunek
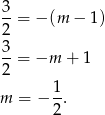
Odpowiedź: C

