Zadanie nr 1205271
Proste prostopadłe 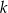 i
i 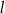 o równaniach
o równaniach 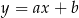 oraz
oraz 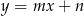 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 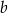 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 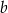 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 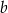 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 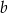 i
i  muszą być dodatnie
muszą być dodatnie
Rozwiązanie
Jeżeli naszkicujemy opisaną sytuację, to powinno być jasne, że obie proste nie mogą przecinać osi 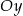 powyżej osi
powyżej osi 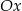 , bo wtedy punkt przecięcia tych prostych ma drugą współrzędną dodatnią.
, bo wtedy punkt przecięcia tych prostych ma drugą współrzędną dodatnią.
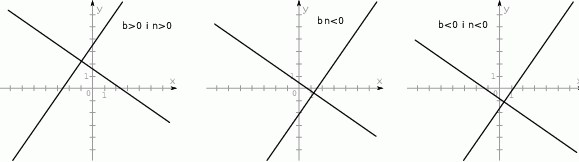
Zatem nie jest możliwe, że jednocześnie 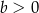 i
i 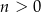 . Może natomiast się zdarzyć, że
. Może natomiast się zdarzyć, że 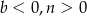 lub
lub 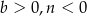 lub wreszcie
lub wreszcie 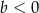 i
i 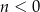 .
.
Odpowiedź: A

