Zadanie nr 6276884
Prosta prostopadła do prostej 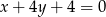 i przechodząca przez początek układu współrzędnych ma równanie
i przechodząca przez początek układu współrzędnych ma równanie
A) 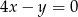 B)
B) 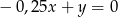 C)
C) 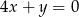 D)
D) 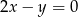
Rozwiązanie
Przekształcamy dane równanie prostej
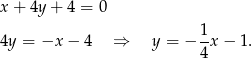
Niech 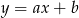 będzie szukaną prostą. Z warunku na prostopadłość prostych otrzymujemy
będzie szukaną prostą. Z warunku na prostopadłość prostych otrzymujemy
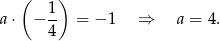
Ponieważ szukana prosta ma przechodzić przez początek układu współrzędnych, więc
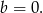
Zatem szukana prosta ma równanie
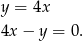
Odpowiedź: A

