Zadanie nr 8868080
Na rysunku przedstawione są dwie proste równoległe 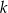 i
i 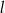 o równaniach
o równaniach 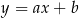 oraz
oraz 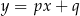 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
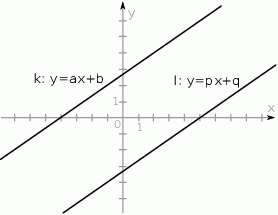
Zatem
A) 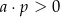 i
i 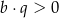 B)
B) 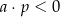 i
i 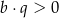
C) 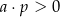 i
i 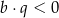 D)
D) 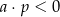 i
i 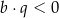
Rozwiązanie
Jeżeli proste są równoległe to mają równe współczynniki kierunkowe, więc
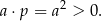
Wiemy ponadto, że przecinają oś 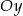 po dwóch różnych stronach początku układu współrzędnych, więc wyrazy wolne
po dwóch różnych stronach początku układu współrzędnych, więc wyrazy wolne 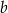 i
i 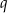 różnią się znakiem. Zatem
różnią się znakiem. Zatem
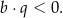
Odpowiedź: C

