Zadanie nr 1213723
Wskaż równanie symetralnej odcinka 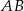 , gdy
, gdy 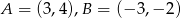 .
.
A) 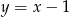 B)
B) 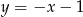 C)
C) 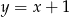 D)
D) 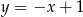
Rozwiązanie
Zaczynamy od rysunku
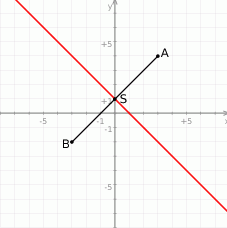
Wyznaczamy równanie prostej 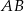
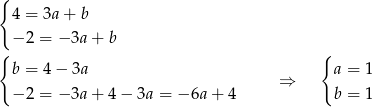
Zatem 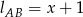 . Obliczamy współrzędną środka odcinka
. Obliczamy współrzędną środka odcinka
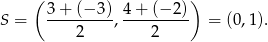
Sposób I
Symetralna musi być prostopadła do prostej 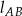 , czyli musi być postaci
, czyli musi być postaci 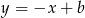 . To pozostawia nas z dwoma odpowiedziami – która z nich jest prawidłowa? – podstawiamy współrzędne punktu
. To pozostawia nas z dwoma odpowiedziami – która z nich jest prawidłowa? – podstawiamy współrzędne punktu 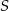 i sprawdzamy.
i sprawdzamy.
Sposób II
Oznaczmy przez 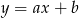 symetralną odcinka
symetralną odcinka 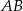 . Korzystając z faktu, że symetralna przechodzi przez środek odcinka i jest prostopadła do prostej
. Korzystając z faktu, że symetralna przechodzi przez środek odcinka i jest prostopadła do prostej 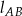 wyznaczamy równanie symetralnej
wyznaczamy równanie symetralnej
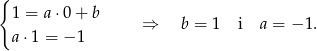
Zatem symetralna ma równanie
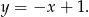
Odpowiedź: D

