/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Różne

Zadanie nr 2096965

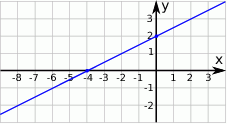
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie

PIC

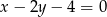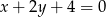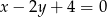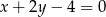
A) x − 2y − 4 = 0 B) x+ 2y + 4 = 0 C) x − 2y + 4 = 0 D) x + 2y − 4 = 0

Wersja PDF

Rozwiązanie

Z podanego wykresu widać, że dana prosta przechodzi przez punkty 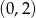(0,2) i (− 4,0) .

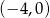Sposób I

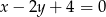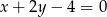Wśród podanych prostych tylko proste x − 2y + 4 = 0 i x + 2y − 4 = 0 przechodzą przez pierwszy punkt. Przez punkt 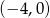(− 4,0) przechodzi tylko pierwsza z nich.

Sposób II

Szukamy prostej w postaci 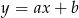y = ax + b przechodzącej przez punkty 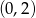(0,2) i (− 4,0) .

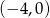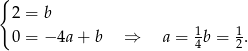
{ 2 = b 0 = − 4a + b ⇒ a = 1b = 1. 4 2

Jest to więc prosta

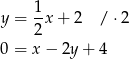
1 y = -x + 2 /⋅ 2 2 0 = x − 2y+ 4

 
Odpowiedź: C

Wersja PDF