Zadanie nr 7319741
Prosta określona wzorem 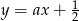 jest symetralną odcinka
jest symetralną odcinka 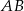 , gdzie
, gdzie 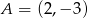 i
i 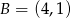 . Wynika stąd, że
. Wynika stąd, że
A) 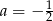 B)
B) 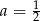 C)
C) 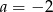 D)
D) 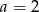
Rozwiązanie
Sposób I
Współczynnik kierunkowy prostej 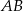 to
to
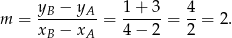
Symetralna odcinka jest do niego prostopadła, więc musi mieć współczynnik kierunkowy równy
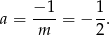
Sposób II
Wyznaczmy równanie prostej 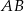 – szukamy równania w postaci
– szukamy równania w postaci 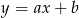 .
.
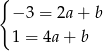
Odejmujemy od drugiego równania pierwsze i mamy
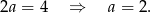
To oznacza, że prosta prostopadła do 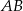 musi mieć współczynnik kierunkowy równy
musi mieć współczynnik kierunkowy równy 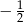 .
.
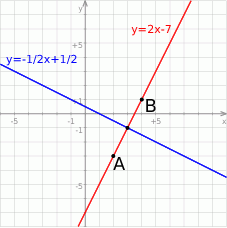
Odpowiedź: A

