Zadanie nr 2089632

Na rysunku przedstawiono fragment prostej o równaniu 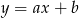y = ax + b .

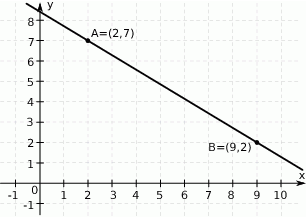
Punkt 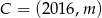C = (2016,m ) leży na tej prostej. Zatem
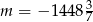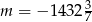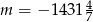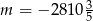
A) m = − 1448 37 B) m = − 1432 37 C) m = − 1431 4 7 D) m = − 28103 5

Rozwiązanie

Szukamy prostej w postaci 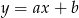y = ax + b . Podstawiając współrzędne punktów 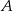i 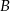do tego równania otrzymujemy układ równań

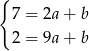
{ 7 = 2a + b 2 = 9a + b

Odejmując od drugiego równania pierwsze (żeby skrócić 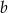) otrzymujemy

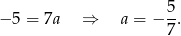
5 − 5 = 7a ⇒ a = − -. 7

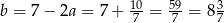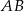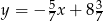Stąd b = 7 − 2a = 7+ 10= 59 = 8 3 7 7 7 i prosta ma równanie 5 3 y = − 7x + 87 .

Podstawiamy teraz w tym równaniu współrzędne punktu .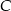

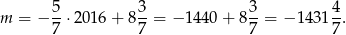
m = − 5-⋅2 016+ 83-= − 1440 + 83-= − 1431 4. 7 7 7 7

Odpowiedź: C

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz