Zadanie nr 2287637
Prosta przechodząca przez punkty 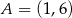 i
i 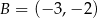 jest określona równaniem
jest określona równaniem
A) 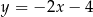 B)
B) 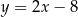 C)
C) 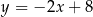 D)
D) 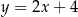
Rozwiązanie
Sposób I
Szukamy prostej w postaci 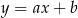 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów  i
i 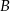 .
.
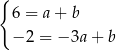
Odejmujemy od pierwszego równania drugie i mamy
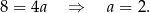
Stąd 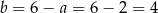 i szukana prosta to
i szukana prosta to 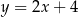 .
.
Sposób II
Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 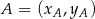 i
i 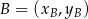 :
:
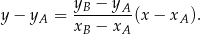
W naszej sytuacji mamy więc
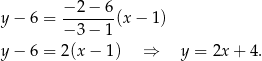
Odpowiedź: D

