Zadanie nr 7339766
Punkt 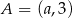 leży poniżej prostej określonej równaniem
leży poniżej prostej określonej równaniem 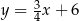 . Stąd wynika, że
. Stąd wynika, że
A) 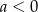 B)
B) 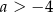 C)
C) 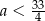 D)
D) 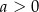
Rozwiązanie
Punkty 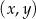 leżące na danej prostej spełniają warunek
leżące na danej prostej spełniają warunek
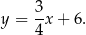
Punkty 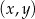 , które leżą poniżej tej prostej mają (dla ustalonej pierwszej współrzędnej
, które leżą poniżej tej prostej mają (dla ustalonej pierwszej współrzędnej  ) mniejszą drugą współrzędną, czyli spełniają warunek
) mniejszą drugą współrzędną, czyli spełniają warunek
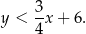
Mamy zatem
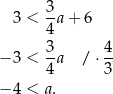
Odpowiedź: B

