/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny

Zadanie nr 2729515

Dodaj do ulubionych
Dodaj do rozwiązanych

Różnica długości podstaw trapezu równoramiennego o kącie ostrym 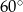∘ 6 0 i ramieniu długości 12 może być równa
A) 6 B) 8 C) 9 D) 12

Rozwiązanie

Szkicujemy obrazek.

PIC

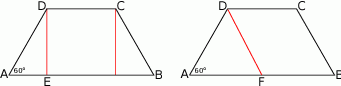
Sposób I

Różnica długości podstaw to podwojona długość odcinka 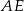AE , a długość tego odcinka możemy wyliczyć z trójkąta prostokątnego AED .

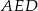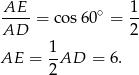
AE--= cos6 0∘ = 1- AD 2 1 AE = --AD = 6 . 2

Zatem różnica podstaw jest równa 12.

Sposób II

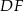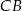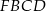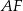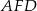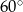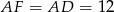Jeżeli dorysujemy odcinek DF równoległy do CB to czworokąt FBCD jest równoległobokiem, więc długość odcinka AF to szukana różnica długości podstaw trapezu. Co więcej, trójkąt AF D jest równoramienny z kątem przy podstawie równym ∘ 60 , więc musi być równoboczny. Zatem AF = AD = 12 .  
Odpowiedź: D

Wersja PDF