Zadanie nr 2908936
Dany jest trapez równoramienny 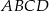 o podstawach
o podstawach 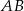 i
i 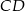 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 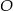 . Jeśli
. Jeśli 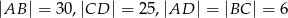 , to
, to
A) 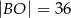 B)
B) 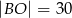 C)
C) 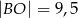 D)
D) 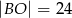
Rozwiązanie
Zaczynamy od rysunku
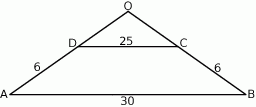
Zauważmy, że trójkąty 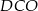 i
i 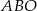 są podobne. Zatem
są podobne. Zatem
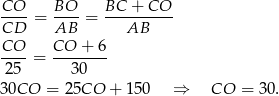
Stąd
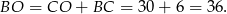
Odpowiedź: A

