/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny

Zadanie nr 4888260

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym podstawy mają długości 8 i 10, a kąt rozwarty ma miarę 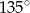135∘ . Obwód trapezu jest równy
A) 24 B) 22 C) 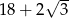√ -- 18 + 2 3 D) √ -- 18 + 2 2

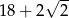
Rozwiązanie

Zaczynamy od rysunku

PIC

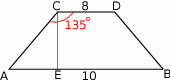
Obliczamy miarę kąta 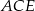ACE

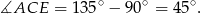
∡ACE = 135∘ − 90 ∘ = 45∘.

Ponieważ trapez jest równoramienny, więc

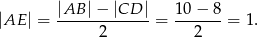
|AE | = |AB-|-−-|CD-| = 1-0−--8 = 1. 2 2

Obliczamy długość ramienia

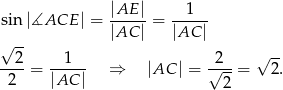
|AE | 1 sin|∡ACE | = -----= ----- -- |AC | |AC | √ 2 1 2 √ -- ----= ----- ⇒ |AC | = √---= 2. 2 |AC | 2

Teraz już łatwo policzyć obwód

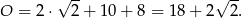
√ -- √ -- O = 2 ⋅ 2 + 10 + 8 = 18+ 2 2.

 
Odpowiedź: D

Wersja PDF