Zadanie nr 5486005
Dany jest trapez równoramienny 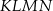 , którego podstawy mają długości
, którego podstawy mają długości 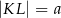 ,
, 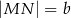 ,
, 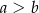 . Kąt
. Kąt 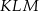 ma miarę
ma miarę 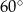 . Długość ramienia
. Długość ramienia 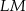 tego trapezu jest równa
tego trapezu jest równa
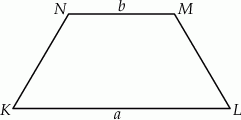
A) 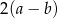 B)
B) 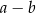 C)
C) 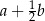 D)
D) 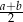
Rozwiązanie
Dorysujmy wysokości 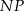 i
i 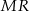 trapezu.
trapezu.
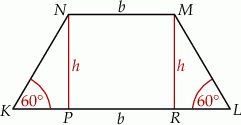
Zauważmy, że
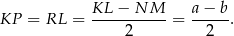
Sposób I
Trójkąt 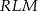 to połówka trójkąta równobocznego o boku długości
to połówka trójkąta równobocznego o boku długości 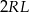 , więc
, więc
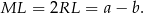
Sposób II
W trójkącie 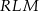 mamy
mamy
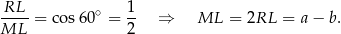
Odpowiedź: B

