Zadanie nr 9178851
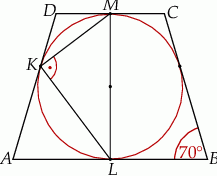
Punkty 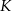 i
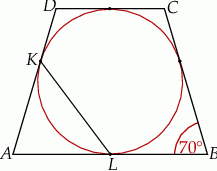
i 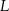 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 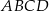 z bokami
z bokami 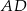 i
i 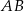 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 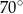 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 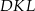 jest równa
jest równa
A) 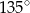 B)
B) 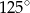 C)
C) 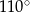 D)
D) 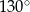
Rozwiązanie
Sposób I
Zauważmy, że trójkąt 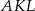 jest równoramienny (bo
jest równoramienny (bo 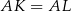 jako odcinki stycznych) oraz
jako odcinki stycznych) oraz
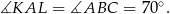
Stąd
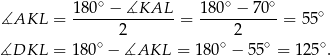
Sposób II
Zauważmy, że jeżeli 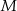 jest punktem styczności okręgu z podstawą
jest punktem styczności okręgu z podstawą 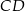 , to odcinek
, to odcinek 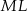 jest średnicą tego okręgu.
jest średnicą tego okręgu.
W szczególności 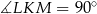 . Ponieważ
. Ponieważ 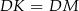 , trójkąt
, trójkąt 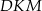 jest równoramienny i
jest równoramienny i
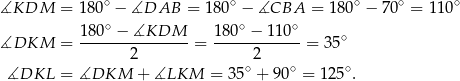
Odpowiedź: B

