Zadanie nr 8212601
Liczba przekątnych jest o 3 większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Rozwiązanie
Sposób I
Liczba przekątnych w 
-kącie jest dana wzorem
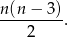
Zatem otrzymujemy równanie
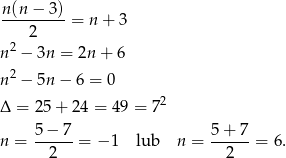
Ponieważ liczba boków jest liczbą większą od 0, więc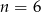 
.
Sposób II
Rysujemy kolejne wielokąty i sprawdzamy, w którym z nich jest spełniony podany warunek.
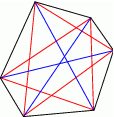
Łatwo sprawdzić, że tak jest w sześciokącie – ma on 9 przekątnych.
Odpowiedź: C
