Zadanie nr 1058199
Punkt 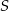 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 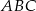 , w którym
, w którym 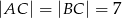 i
i 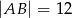 .
.
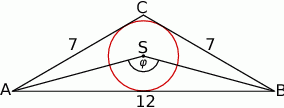
Wówczas miara 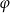 kąta
kąta 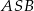 spełnia warunek
spełnia warunek
A) 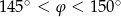 B)
B) 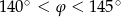 C)
C) 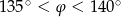 D)
D) 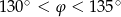
Rozwiązanie
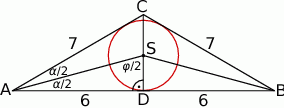
Niech 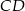 będzie wysokością trójkąta
będzie wysokością trójkąta 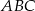 i
i 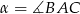 .
.
Wtedy
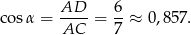
Odczytujemy teraz z tablic, że 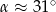 . W takim razie
. W takim razie
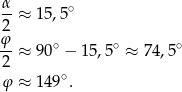
Odpowiedź: A

