Zadanie nr 3886770
Dany jest trójkąt równoramienny 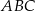 , w którym
, w którym 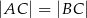 . Na podstawie
. Na podstawie 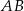 tego trójkąta leży punkt
tego trójkąta leży punkt 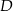 , taki że
, taki że 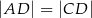 ,
, 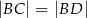 oraz
oraz 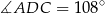 (zobacz rysunek).
(zobacz rysunek).
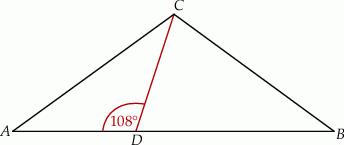
Wynika stąd, że kąt 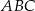 ma miarę
ma miarę
A) 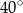 B)
B) 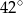 C)
C) 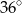 D)
D) 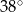
Rozwiązanie
Wiemy, że trójkąty 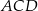 i
i 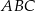 są równoramienne,
są równoramienne,
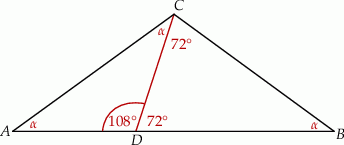
więc jeżeli oznaczymy 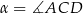 , to
, to
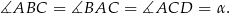
Sposób I
Patrzymy na trójkąt równoramienny 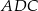 .
.
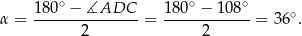
Sposób II
Wiemy, że trójkąt 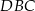 jest równoramienny, więc
jest równoramienny, więc
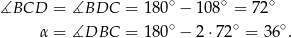
Sposób III
Tak jak poprzednio zauważamy, że
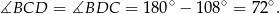
Suma kątów w trójkącie 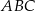 jest równa
jest równa 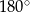 , więc
, więc
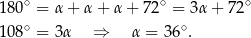
Odpowiedź: C

