Zadanie nr 6537280
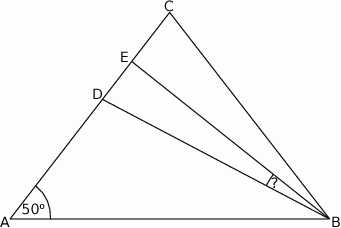
W trójkącie równoramiennym 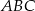 spełnione są warunki:
spełnione są warunki: 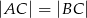 ,
, 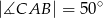 . Odcinek
. Odcinek 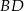 jest dwusieczną kąta
jest dwusieczną kąta 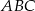 , a odcinek
, a odcinek 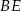 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 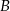 na bok
na bok 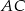 . Miara kąta
. Miara kąta 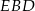 jest równa
jest równa
A) 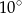 B)
B) 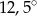 C)
C) 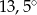 D)
D) 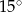
Rozwiązanie
Trójkąt 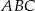 jest równoramienny, więc
jest równoramienny, więc
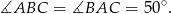
Korzystamy teraz z tego, że trójkąt 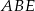 jest prostokątny oraz z tego, że odcinek
jest prostokątny oraz z tego, że odcinek 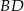 jest dwusieczną kąta
jest dwusieczną kąta 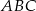 .
.
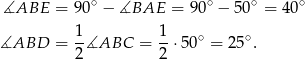
Mamy zatem
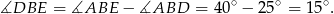
Odpowiedź: D

