Zadanie nr 4557092
W trójkącie 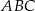 bok
bok 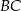 ma długość 13, a wysokość
ma długość 13, a wysokość 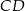 tego trójkąta dzieli bok
tego trójkąta dzieli bok 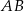 na odcinki o długościach
na odcinki o długościach 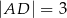 i
i 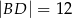 (zobacz rysunek obok).
(zobacz rysunek obok).
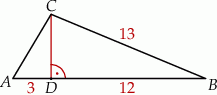
Długość boku 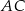 jest równa
jest równa
A) 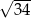 B)
B) 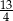 C)
C) 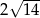 D)
D) 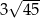
Rozwiązanie
Dwa razy korzystamy z twierdzenia Pitagorasa – pierwszy raz w trójkącie prostokątnym 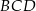 , a drugi raz w trójkącie prostokątnym
, a drugi raz w trójkącie prostokątnym 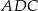 .
.
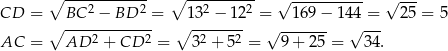
Odpowiedź: A

