Zadanie nr 2413028
Dane są dwa trójkąty podobne 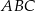 i
i 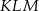 o polach równych – odpowiednio –
o polach równych – odpowiednio – 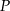 oraz
oraz 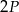 . Obwód trójkąta
. Obwód trójkąta 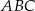 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 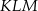 jest równy
jest równy
A) 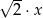 , , | B) 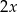 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Rozwiązanie
Jeżeli trójkąty są podobne w skali 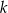 , to stosunek ich obwodów jest równy
, to stosunek ich obwodów jest równy 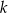 , a stosunek ich pól jest równy
, a stosunek ich pól jest równy 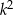 . Zatem stosunek obwodów to pierwiastek ze stosunku ich pól. W naszej sytuacji mamy więc
. Zatem stosunek obwodów to pierwiastek ze stosunku ich pól. W naszej sytuacji mamy więc
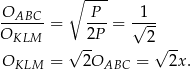
Odpowiedź: A, 2

