Zadanie nr 5703374
Dwa trójkąty podobne mają pola równe odpowiednio 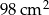 ,
, 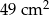 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 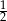 B) 2 C) 4 D)
B) 2 C) 4 D) 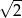
Rozwiązanie
Sposób I
Oznaczmy przez 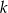 skalę podobieństwa trójkątów. Pole figur zmienia się przy podobieństwie jak kwadrat skali podobieństwa, zatem mamy
skalę podobieństwa trójkątów. Pole figur zmienia się przy podobieństwie jak kwadrat skali podobieństwa, zatem mamy
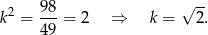
Sposób II
Oznaczmy przez 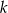 skalę podobieństwa trójkątów. Pamiętamy, że pole powierzchni trójkąta wyraża się wzorem
skalę podobieństwa trójkątów. Pamiętamy, że pole powierzchni trójkąta wyraża się wzorem
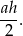
Ponieważ trójkąty z zadania są podobne, więc pole powierzchni drugiego trójkąta wyraża się wzorem
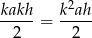
Zauważmy, że pole powierzchni pierwszego trójkąta jest dwa razy mniejsze niż drugiego. Zatem
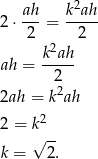
Odpowiedź: D

