/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Dowolny/Różne

Zadanie nr 3422545

Dodaj do ulubionych
Dodaj do rozwiązanych

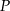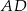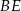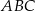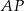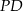Punkt P jest punktem wspólnym środkowych AD i BE w trójkącie ABC . Wówczas odcinki AP i PD mogą mieć długości
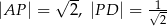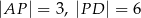
A) √ -- |AP | = 2, |PD | = √1- 2 B) |AP | = 3, |PD | = 6
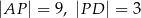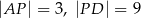
C) |AP | = 9, |P D | = 3 D) |AP | = 3, |P D | = 9

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

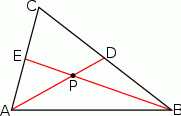
Ponieważ środkowe dzielą się w stosunku 2:1 licząc od wierzchołka, odcinek 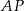AP musi być dwa razy dłuższy od 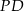P D . Sprawdzając po kolei łatwo zauważyć, że

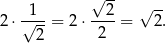
√ -- 1 2 √ -- 2⋅√----= 2 ⋅----= 2. 2 2

 
Odpowiedź: A

Wersja PDF