Zadanie nr 5589283
Mamy cztery urny. W urnie o numerze 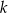 , dla
, dla 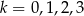 znajduje się
znajduje się 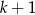 kul białych i
kul białych i 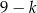 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z 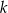 oczkami,
oczkami, 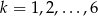 to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby
to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby 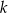 przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 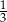 B)
B) 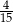 C)
C) 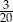 D)
D) 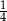
Rozwiązanie
Jeżeli oznaczymy przez 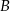 prawdopodobieństwo wylosowania kuli białej w opisanym doświadczeniu losowym, a przez
prawdopodobieństwo wylosowania kuli białej w opisanym doświadczeniu losowym, a przez 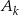 zdarzenie polegające na wyborze urny o numerze
zdarzenie polegające na wyborze urny o numerze 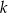 (
(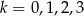 ), to mamy obliczyć prawdopodobieństwo całkowite
), to mamy obliczyć prawdopodobieństwo całkowite
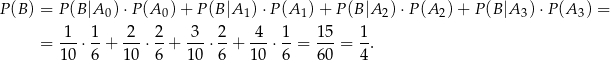
Powyższy rachunek można ładnie zilustrować drzewkiem.
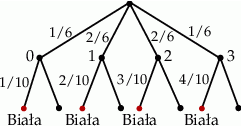
Odpowiedź: D

