/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy 28 maja 2009 Czas pracy: 170 minut
Zadania zamknięte
Liczbę 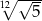 można zapisać inaczej w postaci
można zapisać inaczej w postaci
A) 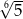 B)
B) 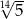 C)
C) 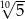 D)
D) 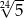
Liczbą odwrotną do 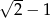 jest
jest
A) 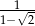 B)
B) 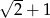 C)
C) 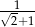 D)
D) 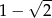
Po dwukrotnej obniżce ceny za każdym razem o 4% buty kosztowały 230,40 zł. Ich cena początkowa to:
A) 250 zł B) 270 zł C) 290 zł D) 202,40 zł
Dziedziną funkcji 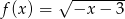 jest zbiór
jest zbiór
A) 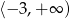 B)
B) 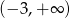 C)
C) 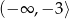 D)
D) 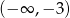
Wykres funkcji określonej na zbiorze liczb rzeczywistych:
A) musi mieć punkt wspólny z osią 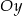 ,
,
B) może mieć dwa punkty wspólne z osią 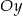 ,
,
C) musi mieć punkt wspólny z osią 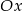 ,
,
D) przechodzi przez początek układu współrzędnych.
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 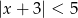 B)
B) 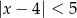 C)
C) 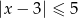 D)
D) 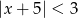
Do zbioru rozwiązań nierówności 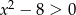 nie należy liczba:
nie należy liczba:
A) -3 B) 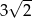 C) 5 D)
C) 5 D) 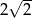
Okrąg o równaniu 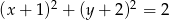 :
:
A) nie przecina osi 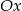 ,
,
B) nie przecina osi 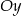 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 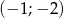 .
.
Środek 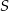 okręgu o równaniu
okręgu o równaniu 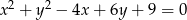 ma współrzędne
ma współrzędne
A) 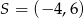 B)
B) 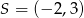 C)
C) 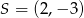 D)
D) 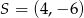
Kąt środkowy okręgu jest większy od kąta wpisanego opartego na tym samym łuku, o
A) 200% B) 150% C) 100% D) 50%
Prosta 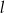 ma równanie
ma równanie 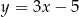 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 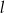 i przechodzącej przez punkt
i przechodzącej przez punkt 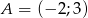 ma postać:
ma postać:
A) 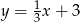 B)
B) 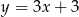 C)
C) 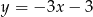 D)
D) 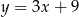
Parabola, która jest wykresem funkcji 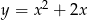 ma z prostą o równaniu
ma z prostą o równaniu 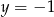
A) dwa punkty wspólne
B) jeden punkt wspólny
C) zero punktów wspólnych
D) trzy punkty wspólne
Funkcja 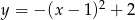 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 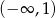 B)
B) 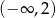 C)
C) 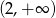 D)
D) 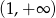
Wiadomo, że 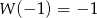 , gdy
, gdy 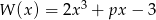 . Zatem wartość współczynnika
. Zatem wartość współczynnika 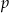 wynosi:
wynosi:
A) 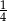 B) -4 C) 4 D) -1
B) -4 C) 4 D) -1
Funkcja 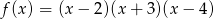 ma
ma
A) 1 miejsce zerowe
B) 2 miejsca zerowe
C) 3 miejsca zerowe
D) nie ma miejsc zerowych
Równanie 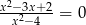 ma:
ma:
A) 2 pierwiastki B) 3 pierwiastki C) 1 pierwiastek D) 4 pierwiastki
Wyrażenie wymierne 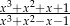 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 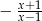 B)
B) 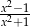 C)
C) 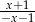 D)
D) 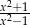
Wzorem ogólnym ciągu geometrycznego w którym 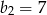 i
i 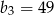 jest:
jest:
A) 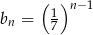 B)
B) 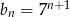 C)
C) 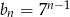 D)
D) 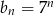
Suma pierwszych 10 wyrazów ciągu o wyrazie ogólnym 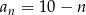 , gdzie
, gdzie 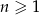 wynosi
wynosi
A) 46 B) 40 C) 45 D) 50
Powierzchnia sześcianu wynosi 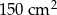 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Zadania otwarte
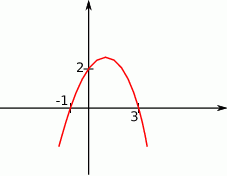
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
Stosując wzory skróconego mnożenia przedstaw w postaci iloczynowej wyrażenie: 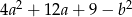 .
.
Wyznacz najmniejszą i największą wartość funkcji: 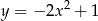 w przedziale
w przedziale 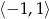 .
.
Znajdź równanie okręgu o środku w punkcie 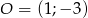 , wiedząc, że okrąg jest styczny do prostej
, wiedząc, że okrąg jest styczny do prostej 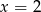 .
.
Rozwiąż równanie 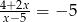 .
.
Oblicz długości boków trójkąta prostokątnego wiedząc, że długości przyprostokątnych różnią się o 9 cm, a jego pole jest równe 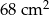 .
.
W biegu narciarskim na 30 km różnica czasów między zwycięzcą i ostatnim zawodnikiem była równa 20 min. Po biegu obliczono, że średnia prędkość zwycięzcy była o 3 km/h większa od prędkości ostatniego biegacza. Oblicz prędkość zwycięzcy.
Na okręgu o promieniu 5 opisano deltoid o obwodzie 60. Oblicz pole deltoidu.
Liczby 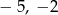 oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego
oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego 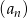 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 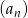 należy do przedziału
należy do przedziału 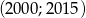 .
.
Belki ułożono warstwami w ten sposób, że na dole jest 50 belek, w warstwie górnej 21, a każda kolejna warstwa zawiera o jedną belkę mniej niż warstwa niższa. Ile belek jest łącznie?

