/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/CKE, OKE, CEN

Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 28 maja 2009 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Dany jest wielomian 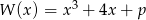W (x) = x3 + 4x + p , gdzie p jest liczbą pierwszą. Wyznacz p wiedząc, że W (x) ma pierwiastek całkowity.

Zadanie 2
(4 pkt)

Stosując własności wartości bezwzględnej rozwiąż nierówność: 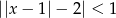||x − 1|− 2| < 1 .

Zadanie 3
(3 pkt)

Liczba 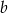b jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 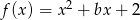f (x) = x2 + bx + 2 jest większa od 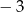− 3 . Wyznacz liczbę b .

Zadanie 4
(4 pkt)

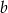Wyznacz drugi, trzeci i czwarty wyraz ciągu określonego wzorem rekurencyjnym:

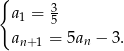
{ a1 = 3 5 an+ 1 = 5an − 3.

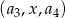Dla wyznaczonych wyrazów znajdź taką liczbę x , aby ciąg (a3,x,a4) był ciągiem geometrycznym.

Zadanie 5
(4 pkt)

Wykaż, że jeżeli 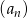(an) jest ciągiem geometrycznym, to ciąg 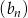(bn) o wyrazie ogólnym określonym wzorem 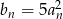2 bn = 5a n też jest ciągiem geometrycznym.

Zadanie 6
(7 pkt)

Długości boków trójkąta prostokątnego o obwodzie 30 cm są pierwszym, piętnastym i siedemnastym wyrazem rosnącego ciągu arytmetycznego. Oblicz pole tego trójkąta.

Zadanie 7
(6 pkt)

Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od końców ramienia pochyłego danego trapezu. Znaleźć pole trapezu.

Zadanie 8
(3 pkt)

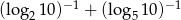Oblicz (log2 10)−1 + (log5 10)−1 .

Zadanie 9
(4 pkt)

Z równania 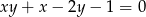xy + x− 2y− 1 = 0 wyznacz 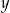y jako funkcję zmiennej x . Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.

Zadanie 10
(7 pkt)

Napisz równanie okręgu stycznego do osi 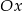Ox układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej 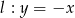l : y = −x i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do l .

Zadanie 11
(3 pkt)

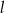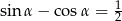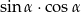Wiedząc, że 1 sin α − cos α = 2 , oblicz wartość wyrażenia sin α ⋅cos α .

Arkusz Wersja PDF
Rozwiązania