/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy styczeń 2009 Czas pracy: 170 minut
Zadania zamknięte
Dana jest funkcja liniowa określona wzorem 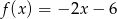 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 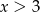 B)
B) 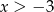 C)
C) 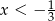 D)
D) 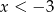
Równanie 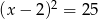 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Funkcja liniowa, której wykres jest równoległy do wykresu funkcji 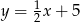 ma wzór:
ma wzór:
A) 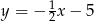 B)
B) 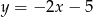 C)
C) 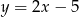 D)
D) 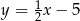
Funkcja kwadratowa o miejscach zerowych 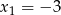 i
i 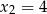 , której wykres przechodzi przez punkt
, której wykres przechodzi przez punkt 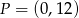 ma wzór:
ma wzór:
A) 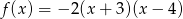
B) 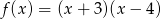
C) 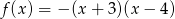
D) 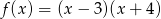
Liczba 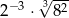 jest równa
jest równa
A) 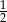 B) 1 C) 2 D) 4
B) 1 C) 2 D) 4
Funkcja 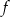 określona jest wzorem
określona jest wzorem
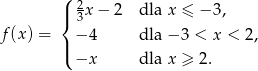
Funkcja ta jest malejąca na przedziale
A) 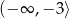 B)
B) 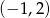 C)
C) 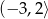 D)
D) 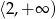
Zbiorem rozwiązań nierówności 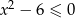 jest
jest
A) 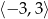 B)
B) 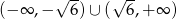 C)
C) 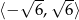 D)
D) 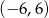
Dany jest trójkąt prostokątny (patrz rysunek).
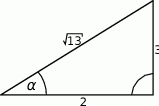
Wartość wyrażenia 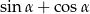 wynosi
wynosi
A) 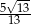 B)
B) 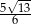 C)
C) 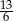 D) 1
D) 1
Dziedziną funkcji 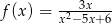 jest zbiór
jest zbiór
A) 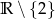 B)
B) 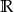 C)
C) 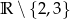 D)
D) 
Rower kosztujący 270 zł sprzedano podczas wyprzedaży za 216 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 80%
Odcinki 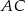 i
i 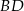 są równoległe.
są równoległe.
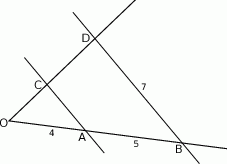
Długości odcinków podane są na rysunku. Długość odcinka 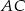 jest równa
jest równa
A) 6 B) 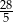 C)
C) 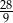 D)
D) 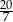
Rozwiązaniem układu równań 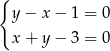 jest para
jest para
A) 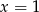 i
i 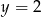 B)
B) 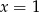 i
i 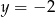 C)
C) 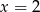 i
i 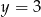 D)
D) 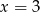 i
i 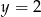
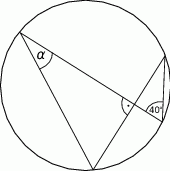
Miara kąta  wynosi
wynosi
A) 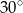 B)
B) 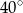 C)
C) 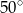 D)
D) 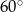
Do wykresu funkcji 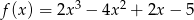 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 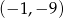 B)
B) 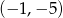 C)
C) 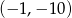 D)
D) 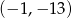
Wyrażenie 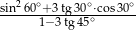 ma wartość
ma wartość
A) 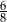 B)
B) 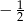 C)
C) 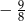 D)
D) 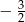
Drzewo o wysokości 12 m rzuca cień o długości 25 m. Miara kąta, jaki tworzy promień słoneczny z powierzchnią ziemi wynosi około
A) 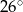 B)
B) 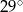 C)
C) 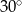 D)
D) 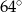
Na rysunku obok
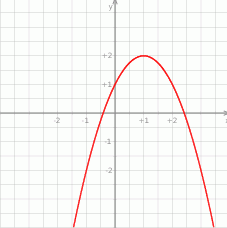
przedstawiony jest wykres funkcji o wzorze
A) 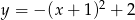 B)
B) 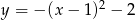 C)
C) 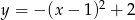 D)
D) 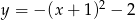
Wyrażenie 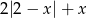 dla
dla 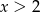 ma wartość
ma wartość
A) 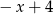 B)
B) 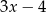 C) 1 D) 5
C) 1 D) 5
Wielomian 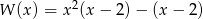 można zapisać w postaci
można zapisać w postaci
A) 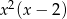 B)
B) 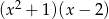 C)
C) 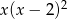 D)
D) 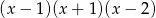
Rozwiązaniem nierówności 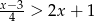 jest zbiór
jest zbiór
A) 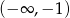 B)
B) 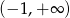 C)
C) 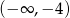 D)
D) 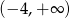
Prosta o równaniu 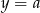 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 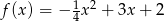 . Wynika stąd, że
. Wynika stąd, że
A) 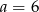 B)
B) 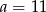 C)
C) 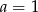 D)
D) 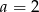
Punkt 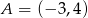 jest początkiem odcinka
jest początkiem odcinka 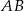 , gdzie
, gdzie 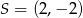 jest jego środkiem. Punkt
jest jego środkiem. Punkt 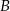 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 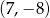 B)
B) 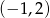 C)
C) 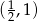 D)
D) 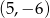
Pole trójkąta o bokach 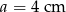 i
i 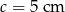 oraz kącie
oraz kącie 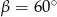 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 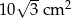 B)
B) 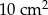 C)
C) 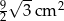 D)
D) 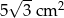
Dane są wielomiany 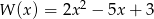 i
i 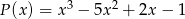 . Wielomian
. Wielomian 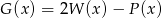 jest równy
jest równy
A) 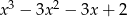 B)
B) 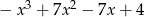 C)
C) 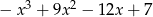 D)
D) 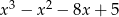
Zadania otwarte
Wykaż, że liczba 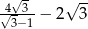 jest liczbą wymierną.
jest liczbą wymierną.
Wyznacz wartość funkcji 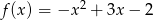 dla argumentu
dla argumentu 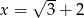 .
.
Rozwiąż równanie 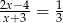 .
.
Rozwiąż nierówność 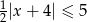 .
.
Dany jest trapez prostokątny (zobacz rysunek).
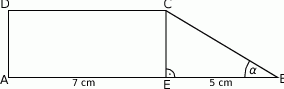
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku  wynosi
wynosi 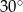 .
.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku tego trójkąta.
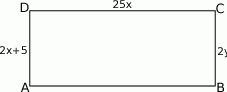
Wyznacz pole narysowanego prostokąta, jeżeli 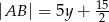 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 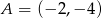 oraz
oraz 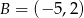 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 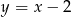 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Suma kwadratów trzech kolejnych liczb naturalnych wynosi 149. Wyznacz te liczby.

