/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki Matura 2010 poziom podstawowy Zestaw P3 (CKE), wrzesień 2009 Czas pracy: 170 minut
Zadania zamknięte
Pole powierzchni całkowitej sześcianu jest równe 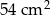 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 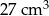 B)
B) 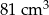 C)
C) 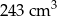 D)
D) 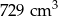
Zbiorem rozwiązań nierówności 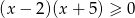 jest
jest
A) 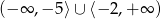
B) 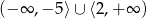
C) 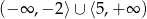
D) 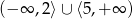
Kąt  jest ostry i
jest ostry i 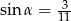 . Wówczas
. Wówczas 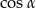 jest równy
jest równy
A) 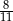 B)
B) 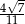 C)
C) 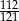 D)
D) 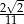
Okrąg opisany na trójkącie równobocznym ma promień równy 6. Wysokość tego trójkąta jest równa
A) 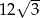 B) 18 C) 9 D)
B) 18 C) 9 D) 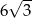
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 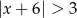 .
.
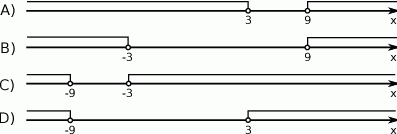
Punkty 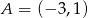 i
i 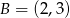 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 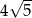 B)
B) 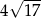 C)
C) 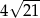 D)
D) 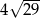
Największą wartością funkcji kwadratowej 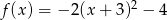 jest
jest
A) 3 B) -2 C) -4 D) 4
Płyta kosztowała 80 zł, a po obniżce 60 zł. O ile procent obniżono cenę płyty?
A) 20% B) 25% C) 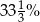 D) 75%
D) 75%
Dany jest okrąg o równaniu 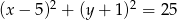 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 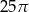 B)
B) 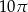 C)
C) 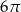 D)
D) 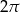
Dane są wielomiany 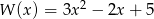 oraz
oraz 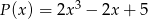 . Wielomian
. Wielomian 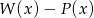 jest równy
jest równy
A) 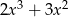 B)
B) 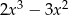 C)
C) 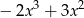 D)
D) 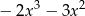
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
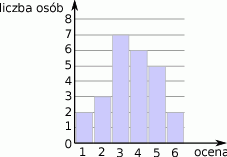
Średnia ocen ze sprawdzianu jest równa
A) 4 B) 3,6 C) 3,5 D) 3
Prosta o równaniu 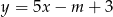 przechodzi przez punkt
przechodzi przez punkt 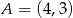 . Wtedy
. Wtedy
A) 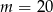 B)
B) 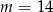 C)
C) 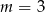 D)
D) 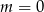
Liczba 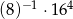 jest równa
jest równa
A) 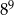 B)
B) 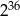 C)
C) 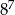 D)
D) 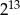
W ciągu geometrycznym drugi wyraz jest równy 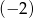 , a trzeci wyraz
, a trzeci wyraz 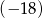 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -9 B) -3 C) 3 D) 9
Piąty wyraz ciągu arytmetycznego jest równy 17, a różnica tego ciągu jest równa 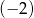 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 9 B) 11 C) 23 D) 25
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Wysokość 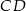 trójkąta równoramiennego
trójkąta równoramiennego 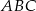 jest równa 8, a ramię
jest równa 8, a ramię 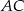 ma długość 10. Podstawa
ma długość 10. Podstawa 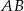 tego trójkąta ma długość
tego trójkąta ma długość
A) 12 B) 6 C) 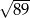 D)
D) 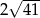
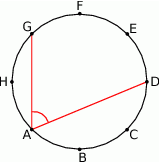
Punkty 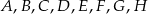 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 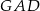 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 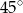 B)
B) 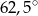 C)
C) 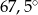 D)
D) 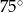
Liczba 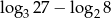 jest równa
jest równa
A) 0 B) 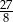 C) 5 D) 19
C) 5 D) 19
Wybieramy jedną liczbę ze zbioru 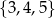 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 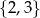 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 3 B) 4 C) 5 D) 6
Zadania otwarte
Rozwiąż nierówność 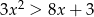 .
.
Rozwiąż równanie 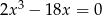 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 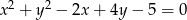 .
.
Wyznacz wartość największą i najmniejszą funkcji kwadratowej 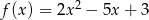 w przedziale
w przedziale 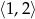 .
.
Udowodnij, że jeśli 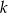 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 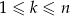 , to
, to 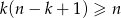 .
.
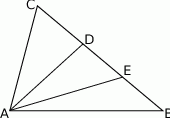
Punkty 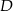 i
i 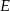 dzielą bok
dzielą bok 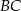 trójkąta
trójkąta 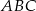 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 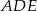 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta 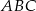 .
.
Kąt  jest ostry
jest ostry 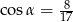 . Oblicz
. Oblicz 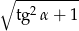 .
.
Sprawdź, czy czworokąt 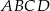 , gdzie
, gdzie 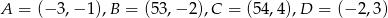 jest równoległobokiem. Odpowiedź uzasadnij.
jest równoległobokiem. Odpowiedź uzasadnij.
Ciąg 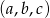 jest arytmetyczny
jest arytmetyczny 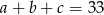 . Ciąg
. Ciąg 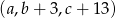 jest geometryczny. Oblicz
jest geometryczny. Oblicz 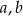 i
i  .
.
Punkty 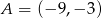 i
i 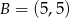 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 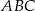 , w którym
, w którym 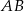 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 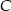 wiedząc, że leży on na osi
wiedząc, że leży on na osi 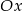 .
.
Za wynajęcie autobusu na wycieczkę uczniowie klasy IA mieli zapłacić 1800 złotych. Ponieważ 4 uczniów zrezygnowało z tej wycieczki, każdy z pozostałych uczniów zapłacił o 15 zł więcej. Oblicz, ilu uczniów jest w klasie IA.

