/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/CKE, OKE, CEN

Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony 28 maja 2009 Czas pracy: 180 minut

Zadanie 1
(3 pkt)

Sprawdź, czy prawdą jest że: 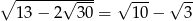∘ ----------- --- 13 − 2√ 30-= √ 10 − √ 3- ?

Zadanie 2
(4 pkt)

Wyniki klasówki z matematyki, której średnia ocen była równa 3,5 przedstawiono w tabeli.

Oceny 12 3 456
Liczba uczniów22x 932
  • Oblicz x .
  • Oblicz medianę danych.

Zadanie 3
(4 pkt)

Funkcja liniowa 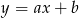y = ax+ b jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia a+ b .

Zadanie 4
(6 pkt)

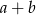Naszkicuj wykres funkcji 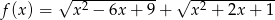√ ------------ √ ------------ f(x) = x2 − 6x+ 9+ x2 + 2x + 1 , a następnie korzystając z otrzymanego wykresu ustal liczbę pierwiastków równania 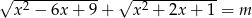√ ------------ √ ------------ x 2 − 6x + 9+ x 2 + 2x + 1 = m w zależności od parametru m , m ∈ R .

Zadanie 5
(3 pkt)

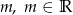Działkę w kształcie trapezu podzielono przekątnymi na 4 działki. Spośród tych czterech działek wskaż dwie o równych polach. Odpowiedź uzasadnij.

Zadanie 6
(4 pkt)

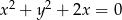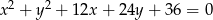Określ wzajemne położenie okręgów: x2 + y2 + 2x = 0 i x 2 + y2 + 1 2x+ 24y + 36 = 0 .

Zadanie 7
(5 pkt)

Dwie cięciwy przecinają się wewnątrz okręgu tak, że odcinki jednej z nich mają długości 8 i 6, a odcinki drugiej pozostają w stosunku 2:3. Podaj długości odcinków drugiej cięciwy.

Zadanie 8
(3 pkt)

Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.

Zadanie 9
(6 pkt)

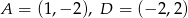Punkty A = (1,− 2), D = (− 2,2) są kolejnymi wierzchołkami trapezu 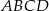ABCD . Prosta 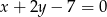x + 2y − 7 = 0 jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.

Zadanie 10
(5 pkt)

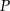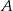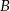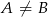Dwa okręgi są styczne zewnętrznie w punkcie P . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach A i B (A ⁄= B ). Wykaż, że kąt 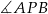∡AP B jest prosty.

Zadanie 11
(3 pkt)

Rozwiąż nierówność liniową 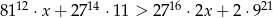8112 ⋅x + 27 14 ⋅11 > 2 716 ⋅2x + 2 ⋅921 .

Zadanie 12
(4 pkt)

W pewnej klasie dziewczęta stanowiły 25% liczby uczniów. Do klasy przybyła jedna osoba i wówczas odsetek dziewcząt wzrósł do 28%. Ilu chłopców jest w tej klasie?

Arkusz Wersja PDF
Rozwiązania