/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 20 marca 2010 Czas pracy: 170 minut
Zadania zamknięte
Kwiatek z doniczką kosztował 50 zł, ale doniczka zdrożała o 10%, a kwiatek zdrożał o 20%. Jeżeli nowa cena kwiatka z doniczką wynosi 56,5 złotego, to aktualna cena doniczki to
A) 42 B) 38,5 C) 35 D) 35,5
Ile liczb wymiernych znajduje się w zbiorze
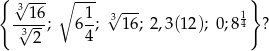
A) 2 B) 3 C) 4 D) 5
Nierówność 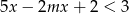 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 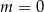 B)
B) 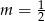 C)
C) 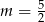 D)
D) 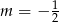
Przybliżenie liczby 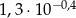 jest równe 0,5175393. Przybliżeniem liczby
jest równe 0,5175393. Przybliżeniem liczby 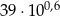 z dokładnością do 3 miejsca po przecinku jest liczba
z dokładnością do 3 miejsca po przecinku jest liczba
A) 15,526 B) 1552,618 C) 155,262 D) 1552,617
Drugi wyraz ciągu 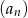 danego wzorem
danego wzorem 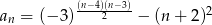 jest równy
jest równy
A) 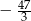 B)
B) 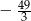 C) -13 D) -19
C) -13 D) -19
Równania 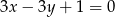 i
i 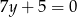 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe
B) są równoległe
C) przecinają się pod kątem 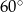
D) przecinają się pod kątem 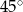
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 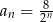 , gdzie
, gdzie 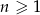 jest równy
jest równy
A) 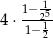 B)
B) 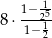 C)
C) 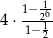 D)
D) 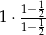
Pole prostokąta przedstawionego na rysunku jest równe 20. Zatem
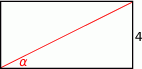
A) 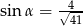 B)
B) 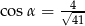 C)
C) 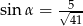 D)
D) 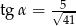
Do wykresu funkcji 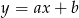 należą punkty
należą punkty 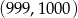 oraz
oraz 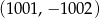 . Wówczas
. Wówczas
A) 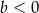 B)
B) 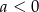 C)
C) 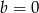 D)
D) 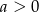
Liczba rozwiązań równania 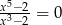 jest równa
jest równa
A) 0 B) 1 C) 2 D) 5
Dana jest funkcja kwadratowa 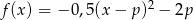 , gdzie
, gdzie 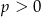 . Wówczas
. Wówczas
A) funkcja osiąga największą wartość równą 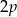 ;
;
B) funkcja ma dwa różne miejsca zerowe;
C) wierzchołek paraboli będącej wykresem 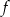 należy do prostej o równaniu
należy do prostej o równaniu 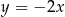 ;
;
D) dla 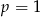 funkcja jest rosnąca w całej swojej dziedzinie.
funkcja jest rosnąca w całej swojej dziedzinie.
Liczby 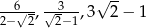 są kolejnymi wyrazami ciągu
są kolejnymi wyrazami ciągu
A) arytmetycznego B) geometrycznego C) rosnącego D) malejącego
Przekątne rombu mają długości 8 i 14. Obwód tego rombu jest równy
A) 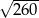 B)
B) 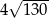 C)
C) 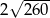 D)
D) 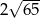
Rozwiązaniem nierówności 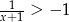 jest zbiór
jest zbiór
A) 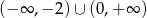
B) 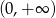
C) 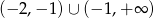
D) 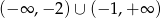
Jeżeli 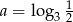 i
i 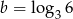 , to liczba
, to liczba 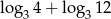 jest równa
jest równa
A) 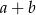 B)
B) 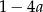 C)
C) 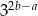 D)
D) 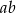
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 24 B) 48 C) 120 D) 60
Długość boku, długość przekątnej oraz pole kwadratu są kolejnymi wyrazami ciągu geometrycznego. Iloraz tego ciągu jest
A) liczbą niewymierną
B) liczbą całkowitą
C) liczbą z przedziału 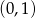
D) wymierną niecałkowitą
Równanie 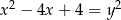 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę B) okrąg C) punkt D) dwie proste
Suma współczynników wielomianu 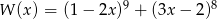 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 0 B) 1 C) 2 D) 3
Jeżeli środek okręgu opisanego na trójkącie leży na wysokości trójkąta, to trójkąt ten musi być
A) równoboczny B) równoramienny C) prostokątny D) rozwartokątny
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 37035 B) 13629 C) 17023 D) 26919
W pewnej klasie, w której jest dwa razy więcej dziewczynek niż chłopców, średnia wzrostu wszystkich chłopców jest równa 157 cm, a średnia wzrostu wszystkich dziewczynek jest równa 160 cm. Średni wzrost uczniów tej klasy jest równy
A) 158 cm B) 158,5 cm C) 159 cm D) 159,5 cm
Jeżeli 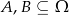 oraz
oraz 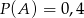 i
i 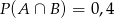 to prawdopodobieństwo
to prawdopodobieństwo 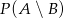 jest równe
jest równe
A) 0,6 B) 0,4 C) 1 D) 0
Punkty 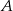 oraz
oraz 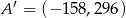 są symetryczne względem prostej
są symetryczne względem prostej 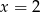 . Wówczas
. Wówczas
A) 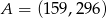 B)
B) 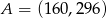 C)
C) 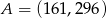 D)
D) 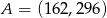
Zadania otwarte
Niech 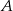 będzie zbiorem rozwiązań równania
będzie zbiorem rozwiązań równania 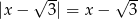 ,
, 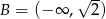 oraz
oraz 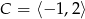 . Wyznacz zbiór
. Wyznacz zbiór 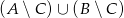 .
.
Oblicz wartość wyrażenia 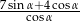 jeżeli
jeżeli  jest takim kątem ostrym, że
jest takim kątem ostrym, że 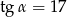 .
.
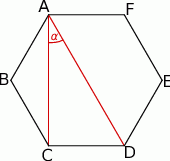
Oblicz miarę kąta  jaki tworzą przekątne
jaki tworzą przekątne 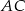 i
i 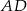 sześciokąta foremnego.
sześciokąta foremnego.
Dwa okręgi o środkach 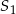 i
i 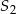 przecinają się w punktach
przecinają się w punktach 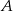 i
i 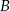 , przy czym punkty
, przy czym punkty 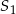 i
i 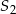 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 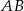 .
.
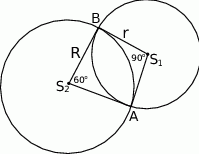
Miary kątów 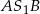 i
i 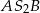 wynoszą odpowiednio
wynoszą odpowiednio 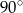 i
i 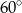 . Wyznacz stosunek
. Wyznacz stosunek 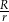 długości promieni tych okręgów.
długości promieni tych okręgów.
Cena produktu po podniesieniu stawki VAT z 7% do 22% wzrosła o 90 zł. Ile jest równa nowa cena produktu?
Okrąg dopisany do boku 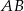 trójkąta
trójkąta 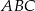 to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków
to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków 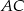 i
i 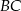 .
.
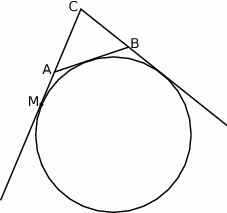
Wykaż, że jeżeli 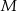 jest punktem styczności tego okręgu z przedłużeniem boku
jest punktem styczności tego okręgu z przedłużeniem boku 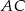 to długość odcinka
to długość odcinka 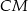 jest równa połowie obwodu trójkąta
jest równa połowie obwodu trójkąta 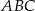 .
.
Zbiornik wodny o objętości 14700 litrów napełniono w całości wodą w następujący sposób. W ciągu pierwszej godziny nalano 800 litrów wody, a w ciągu każdej kolejnej godziny nalewano o 10 litrów mniej. Przez ile godzin napełniano zbiornik?
Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 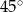 obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
Ze zbioru liczb trzycyfrowych, które nie mają dwóch takich samych cyfr losujemy jedną liczbę. Jakie jest prawdopodobieństwo otrzymania liczby, której iloczyn cyfr jest liczbą niezerową podzielną przez 7?

