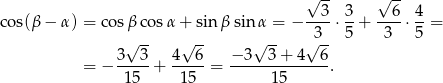/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych/Różne

Zadanie nr 7074037

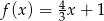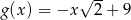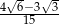Wykaż, że cosinus kąta przecięcia się wykresów funkcji 4 f(x) = 3x + 1 i √ -- g (x ) = −x 2 + 9 jest równy √ - √- 4--6−-3-3 15 .

Wersja PDF

Rozwiązanie

Oczywiście na początku szkicujemy obrazek.

PIC

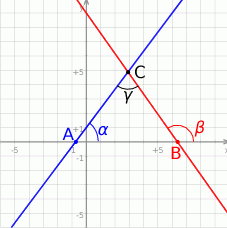
Sposób I

Zauważmy, że korzystając ze wzoru na tangens różnicy, dość łatwo jest wyliczyć tangens interesującego nas kąta. Z trójkąta 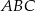ABC łatwo zauważyć, że

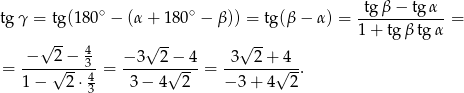
∘ ∘ -tgβ-−--tg-α- tg γ = tg (1 80 − (α+ 180 − β)) = tg (β− α) = 1 + tg βtg α = √ -- 4 √ -- √ -- -−---2−--3- −-3--2-−-4- -3--2-+-4-- = 1 − √ 2-⋅ 4 = 3 − 4√ 2- = − 3+ 4√ 2. 3

Naturalne teraz byłoby wyliczenie z tego tangens cosinusa, ale my zrobimy inaczej. Z podanego w zadaniu cosinusa wyliczymy tangens i sprawdzimy, że jest on równy powyższemu wyrażeniu. Liczymy najpierw sinus

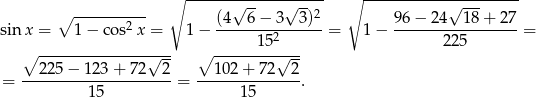
∘ ------√------√----- ∘ ------------√--------- ∘ -------2-- (4--6-−-3--3)2- 96-−-2-4--18+--27 sin x = 1− cos x = 1− 152 = 1 − 225 = ∘ ---------------√--- ∘ --------√--- 225 − 123 + 72 2 102 + 72 2 = ---------1-5--------- = ------15-------.

Zatem tangens jest równy

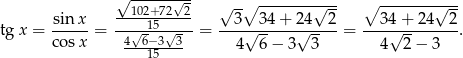
√ ------√-- ∘ ----------- ∘ ----------- sin x --102+72-2- √ 3- 34+ 24√ 2- 34 + 24 √ 2- tg x = ----- = --√-15-√---= ----√------√-----= ---√---------. co sx 4--61−53-3 4 6− 3 3 4 2 − 3

Pozostało porównać to z wcześniej otrzymanym wyrażeniem.

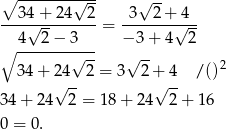
∘ -------√--- √ -- --34√-+-24--2-= -3--2-+√4-- 4 2 − 3 − 3 + 4 2 ∘ -------√--- √ -- 34 + 24 2 = 3 2+ 4 / ()2 √ -- √ -- 3 4+ 24 2 = 18 + 24 2+ 16 0 = 0.

Zatem wszystko się zgadza. Zauważmy, że mogliśmy równość podnieść stronami do kwadratu, bo obie strony były dodatnie.

Sposób II

Tak jak w poprzednim sposobie zauważamy, że 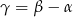γ = β− α . Tym razem skorzystamy jednak ze wzoru na cosinus różnicy.

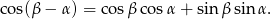
co s(β− α) = cos β cosα + sin βsin α.

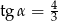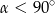Wiemy, że 4 tg α = 3 oraz α < 9 0∘ . Mamy zatem

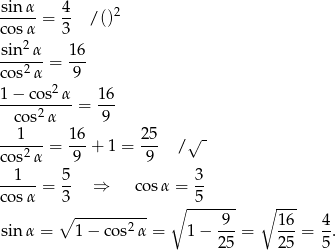
sin-α = 4- / ()2 cos α 3 sin2 α 16 ---2-- = --- cos α 9 1-−-cos2-α 16- cos2 α = 9 1 16 2 5 √ - ---2-- = ---+ 1 = --- / cos α 9 9 --1-- = 5- ⇒ cosα = 3- cos α 3 -5----- --- ∘ ---------- ∘ 9 ∘ 16 4 sin α = 1 − co s2α = 1− ---= ---= -. 25 25 5

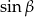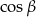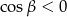Podobnie wyliczamy sin β i co sβ . Musimy jedynie pamiętać, że cosβ < 0 .

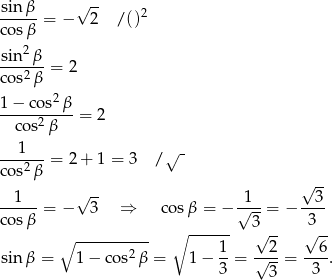
√ -- sin-β = − 2 / ()2 co sβ sin2 β ------ = 2 co s2β 1 − co s2 β ------2--- = 2 co s β ---1-- √ - co s2β = 2+ 1 = 3 / √ -- --1-- √ -- -1-- --3- co sβ = − 3 ⇒ co sβ = − √ 3-= − 3 ∘ ---------- ∘ ------ √ -- √ -- 2 1- --2- --6- sin β = 1− cos β = 1 − 3 = √ 3 = 3 .

Mamy więc

√ -- √ -- 3 3 6 4 cos(β − α) = co sβ cosα + sin β sin α = − ----⋅ --+ ----⋅--= √ -- √ -- √ -- √3-- 5 3 5 = − 3--3-+ 4--6-= −-3--3-+-4--6-. 15 15 15
Wersja PDF