Zadanie nr 3181314
Oblicz całkę 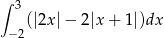 .
.
Rozwiązanie
Podzielimy przedział całkowania na części tak, aby móc opuścić wartości bezwzględne.
![∫ 3 (|2x |− 2 |x + 1|)dx = − 2 ∫ − 1 ∫ 0 ∫ 3 = (|2x |− 2|x + 1|)dx + (|2x |− 2|x + 1|)dx + (|2x |− 2|x + 1|)dx = ∫− 2 ∫ − 1 ∫ 0 − 1 0 3 = − 2 (− 2x + 2x+ 2)dx + − 1(− 2x− 2x − 2)dx + 0 (2x − 2x − 2)dx = ∫ − 1 ∫ 0 ∫ 3 = 2dx + (− 4x − 2)dx + (− 2)dx = − 2 − 1 0 −1 [ 2 ]0 3 = [2x]−2 + − 2x − 2x + [− 2x]0 = −1 = (− 2+ 4)+ (0− 0)+ (−6 − 0 ) = − 4.](https://img.zadania.info/zad/3181314/HzadR0x.gif)
Odpowiedź: -4
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 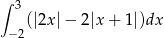 .
.
Podzielimy przedział całkowania na części tak, aby móc opuścić wartości bezwzględne.
![∫ 3 (|2x |− 2 |x + 1|)dx = − 2 ∫ − 1 ∫ 0 ∫ 3 = (|2x |− 2|x + 1|)dx + (|2x |− 2|x + 1|)dx + (|2x |− 2|x + 1|)dx = ∫− 2 ∫ − 1 ∫ 0 − 1 0 3 = − 2 (− 2x + 2x+ 2)dx + − 1(− 2x− 2x − 2)dx + 0 (2x − 2x − 2)dx = ∫ − 1 ∫ 0 ∫ 3 = 2dx + (− 4x − 2)dx + (− 2)dx = − 2 − 1 0 −1 [ 2 ]0 3 = [2x]−2 + − 2x − 2x + [− 2x]0 = −1 = (− 2+ 4)+ (0− 0)+ (−6 − 0 ) = − 4.](https://img.zadania.info/zad/3181314/HzadR0x.gif)
Odpowiedź: -4
