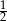/Studia/Analiza/Całki oznaczone/Z logarytmem

Zadanie nr 3713113

Oblicz całkę 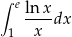∫ e ln x ----dx 1 x .

Wersja PDF

Rozwiązanie

Sposób I

Liczymy najpierw całkę nieoznaczoną (przez podstawienie)

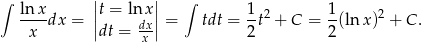
| | ∫ lnx |t = ln x| ∫ 1 2 1 2 ----dx = || dx|| = tdt = -t + C = -(ln x) + C. x dt = x 2 2

Pozostało policzyć całkę oznaczoną

∫ e [ ]e ln-xdx = 1-(lnx)2 = 1. 1 x 2 1 2

Sposób II

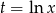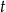Podstawiamy t = ln x , ale musimy pamiętać, że jeżeli x zmienia się w przedziale [1,e] , to t będzie zmieniać się przedziale [0 ,1 ] .

∫ e | | ∫ 1 [ ]1 ln-x-dx = ||t = ln x|| = tdt = 1t2 = 1. 1 x |dt = dxx| 0 2 0 2

Sposób III

Całkujemy przez części

∫ | | ∫ e lnx- ||u ′ = 1x v = lnx || [ 2]e e ln-x- 1 x dx = |u = lnx v ′ = 1 | = (ln x) 1 − 1 x dx = ∫ e x = 1 − ln-x-dx. 1 x

Zatem

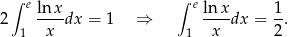
∫ eln x ∫ elnx 1 2 -x--dx = 1 ⇒ -x--dx = 2. 1 1

 
Odpowiedź: 1 2

Wersja PDF